WordRLe

Please be patient, the model is hosted on the free tier of huggingface spaces, and only given CPU access.

I wanted to see if I could teach a transformer model to play the popular game of Wordle. Wordle is a word-guessing game, where the objective is to guess a hidden five-letter word in six attempts or fewer. The user takes turns guessing valid five-letter words until they either run out of guesses or find the correct word. To help guide the player, the game provides feedback in the form of colors. Each character in a guess gets assigned a color based on the target word. Characters in the right position, that is, in the same index as the target word, are green. Characters present in the target word but in the wrong index are colored yellow, and characters that are not present in the target word remain black.

This poses an interesting problem space for reinforcement learning, especially on the character level. The model not only needs to be able to form valid English words, but it must also leverage learned rules of the game in order to complete it.

I initially wanted to use Proximal Policy Optimization to teach the agent how to play the game. However, after spending some time on this approach, I realized it was very difficult for the model to learn. Even on a simplified game of only a single word, the model still struggled. It would often collapse to guessing a single letter or a few random letters.

The reward structure was relatively simple: a positive reward for getting a green, a smaller positive reward for guessing a yellow, and a negative reward for guessing a letter not in the target word. I tweaked this over time, trying to find some combination that worked. But the simplest reward structure often performed the "best" (even if the best wasn't very good).

I decided to move to an "offline" reinforcement learning approach. I created synthetic games based on a somewhat optimal playing of Wordle. The first guess was randomly selected from the pool of valid words. The game provides feedback in the form of greens, yellows, and blacks. The possible words were filtered based on the feedback, such that the next guessed word needed to have a green letter in previously found positions, yellow letters needed to be present (but not in the same spot), and black letters couldn't be present. Then, on guesses from 3 to 6, the correct word would be inserted in the final spot.

This created a lot of possible data for the model to learn. Using causal attention and cross-entropy loss, the model learned which letter to predict based on the previous state space. Through training, I tracked the model's loss and, as validation, the number of games it won.

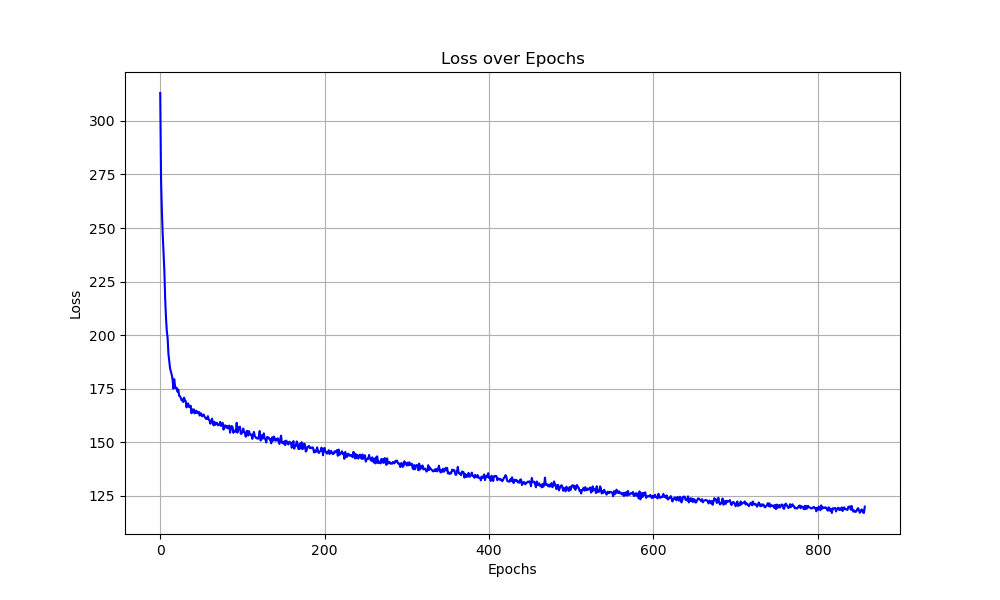
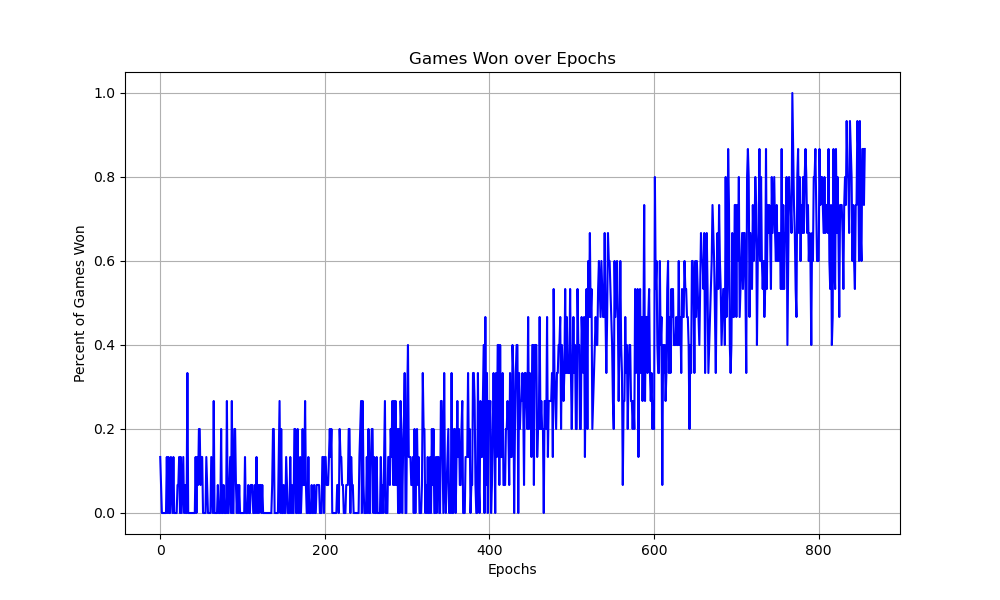
The model trained for a maximum of 1,000 epochs, with an early stopping criterion of 20 epochs with no loss improvement. Each epoch, the model would play 100 synthetic games. After the epoch was complete, the model would play 15 games of Wordle to track its performance over time.

Using a purely greedy approach, the model can properly guess the final word 80% of the time. Even after improved training and larger model sizes, the model was not able to beat this benchmark. So I introduced beam searching. Beam searching is a decoding method used by LLMs to approximate the most optimal sequence of tokens. Unlike the greedy approach, which selects the highest probability token each time, beam search keeps a number of sequences (or beams) and tracks the cumulative log probability of the sequence, pruning out less probable sequences.

With a beam search width of 4, the model can solve 90% of games. As a final improvement, and as a way to make the model play more like a human, I added a random value (between 1 beam and 8 beams) for the beam width at each word generation, which brought the number of games solved to 95%. The improvement likely comes from the trade-off between exploration and exploitation. A fixed beam width of 4 may sometimes prune out optimal sequences too early, while wider beams (5-8) increase the chances of finding better solutions. On the other hand, occasionally using a smaller beam width (1-3) encourages diversity in predictions, preventing the model from always converging to the same strategies. By allowing the beam width to vary, the model benefits from a mix of quick approximate solutions and deeper searches, leading to a higher overall success rate. While my evaluation showed a 95% success rate, I suspect the true performance may be slightly higher, though further testing would be needed.

In the future, I'd like to use PPO for reinforcement learning as a baseline. Right now, the model does a lot of things well. While it's not perfect, it will keep green characters in place and guess yellow ones in different locations. Additionally, one of the model's most frequent starting words is "salep," which is very close to one of the optimal starting words, "salet," which was found by 3Blue1Brown during his investigation into solving Wordle with entropy.